Do you ever look up at the night sky, and feel absolutely disoriented at the size of it all? How far does space stretch, does it ever end? Could something be infinitely big? How would that even be possible?
For years, I could not wrap my mind around this endlessness. The concept of infinity became a personal obsession, it plagued my mind. I made it my quest to comprehend infinity - and surprisingly, I did it. I’m going to share the thought experiment that helped me achieve this.
It all started the day I began studying fractals - those infinitely complex patterns that are self-similar across different scales. There was a particular fractal that piqued my interest - the Mandelbrot set. In its exploration, I was led to a series of thoughts that completely changed my perspective on the universe.

The Mandelbrot Set
For those unfamiliar, here is an overview of the Mandelbrot Set.
The Mandelbrot Set is the set of complex numbers \(c\) for which the function \(\\f_c(z) = z^2 + c\) remains bounded when iterated from \(z = 0\). I.e we repeatedly apply the function starting from zero, and see if the sequence spirals into infinity or not.
The Algorithm:
-
Start with \(z = 0\)
-
Pick a complex number \(c\)
-
Repeatedly apply the function \(\\f_c(z) = z^2 + c\)
-
If the magnitude of \(z_n\) exceeds 2 at any point, the sequence wil tend to infinity, and \(c\) is not in the set
-
Otherwise, the sequence stays bounded, and \(c\) is in the set
Here’s how the iteration unfolds:
$$ z_0 = 0 $$
$$ z_1 = z_0^2 + c $$
$$ z_2 = z_1^2 + c $$
$$ ⋮ $$
$$ z_{n+1} = z_n^2 + c $$
When plotted on a complex plane, the Mandelbrot Set forms its distinctive shape, resembling a series of connected bulbs, symmetric across the real axis. It spans approximately between \(-2\) and \(0.47\) on the real axis and \(-1.12i\) and \(1.12i\) on the imaginary axis.
What makes the Mandelbrot Set so interesting is that it is infinitely intricate. The more you zoom into its edges, the more endless variations of similar patterns are revealed.
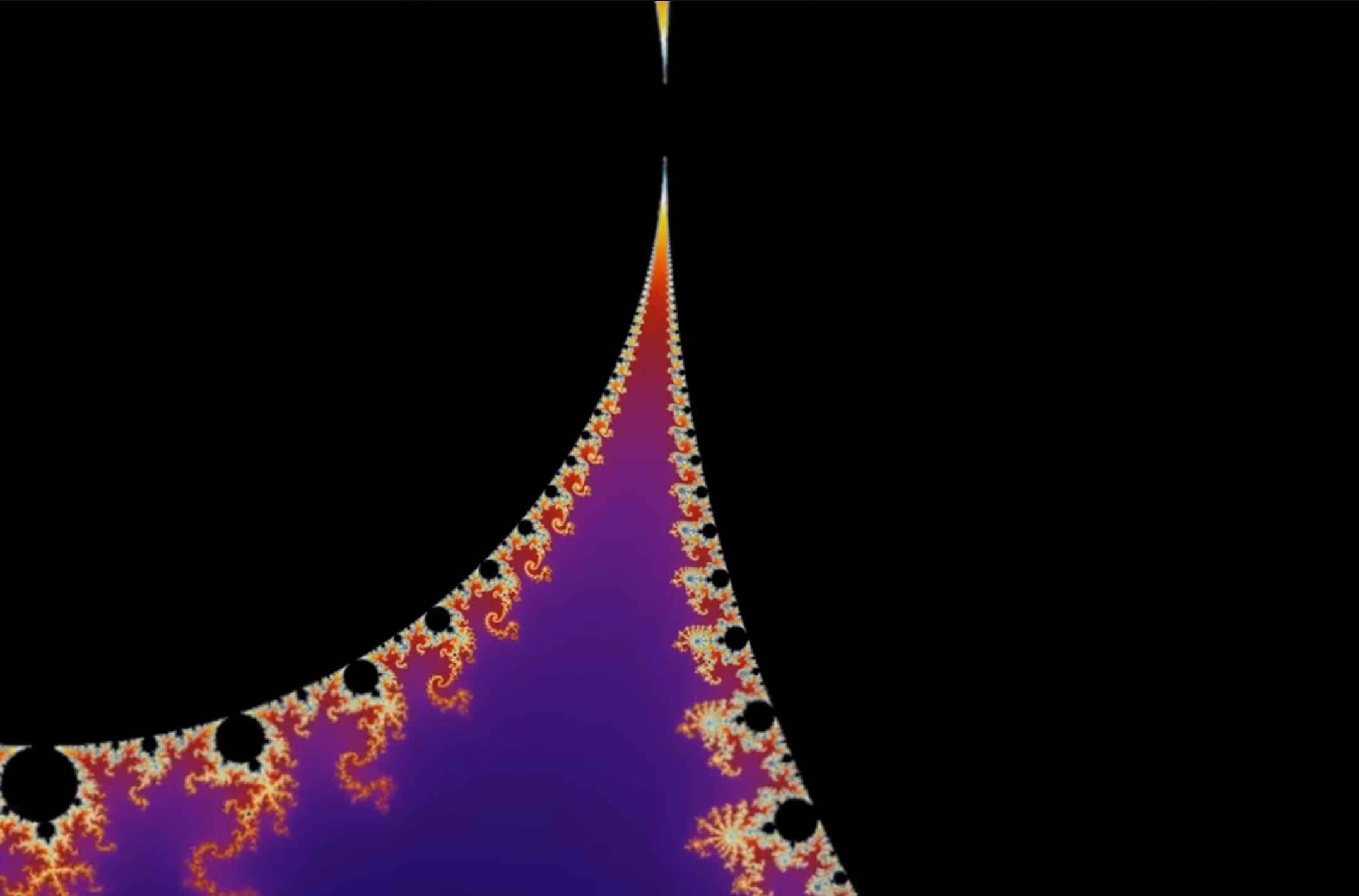

Paradox
Here we are presented with a paradox: the Mandelbrot Set clearly has a finite area - we know that the area is greater than \(0\), and less than a rectangle that would contain it (its surface area has been estimated to be \(1.506591\) square units, though the exact area remains a topic of research). Yet, it has an infinite perimeter - the boundary becomes increasingly intricate the further we zoom in. It is an infinite complexity contained within finite bounds.
This highlights how infinity can exist within finite constraints when we cross dimensional boundaries. Here, the infinite perimeter of the one-dimensional (topological dimension) boundary exists comfortably within a finite two-dimensional area.
Extending to other dimensions
To build on this, let’s start from the beginning.
Consider a simple line segment – finite in length. Within this one-dimensional line, we can fit an infinite number of zero-dimensional points.
Moving up a dimension, fractals such as the Mandelbrot Set show us how an infinite one-dimensional boundary can exist within a finite two-dimensional area. Other examples include the Koch snowflake, and the Sierpinski Triangle.
Increase the dimensions once more, we get three-dimensional fractals like the Mandelbulb or the Menger Sponge. The Mandelbulb, for instance, has a finite, non-zero volume and an infinite surface area.
We observe a pattern: each higher-dimensional level can contain infinite complexity from the dimension below it. That is, an \((𝑛+1)\)-dimensional shape can have an infinite \(𝑛\)-dimensional boundary.
Conclusion
Following this logic: could our three-dimensional universe be the “surface” of a finite higher dimensional space? The infinity we observe might not be a paradox, but a natural consequence of fractal properties.